MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing
Por um escritor misterioso
Last updated 13 abril 2025


Gradient Descent For Mutivariate Linear Regression - Stack Overflow
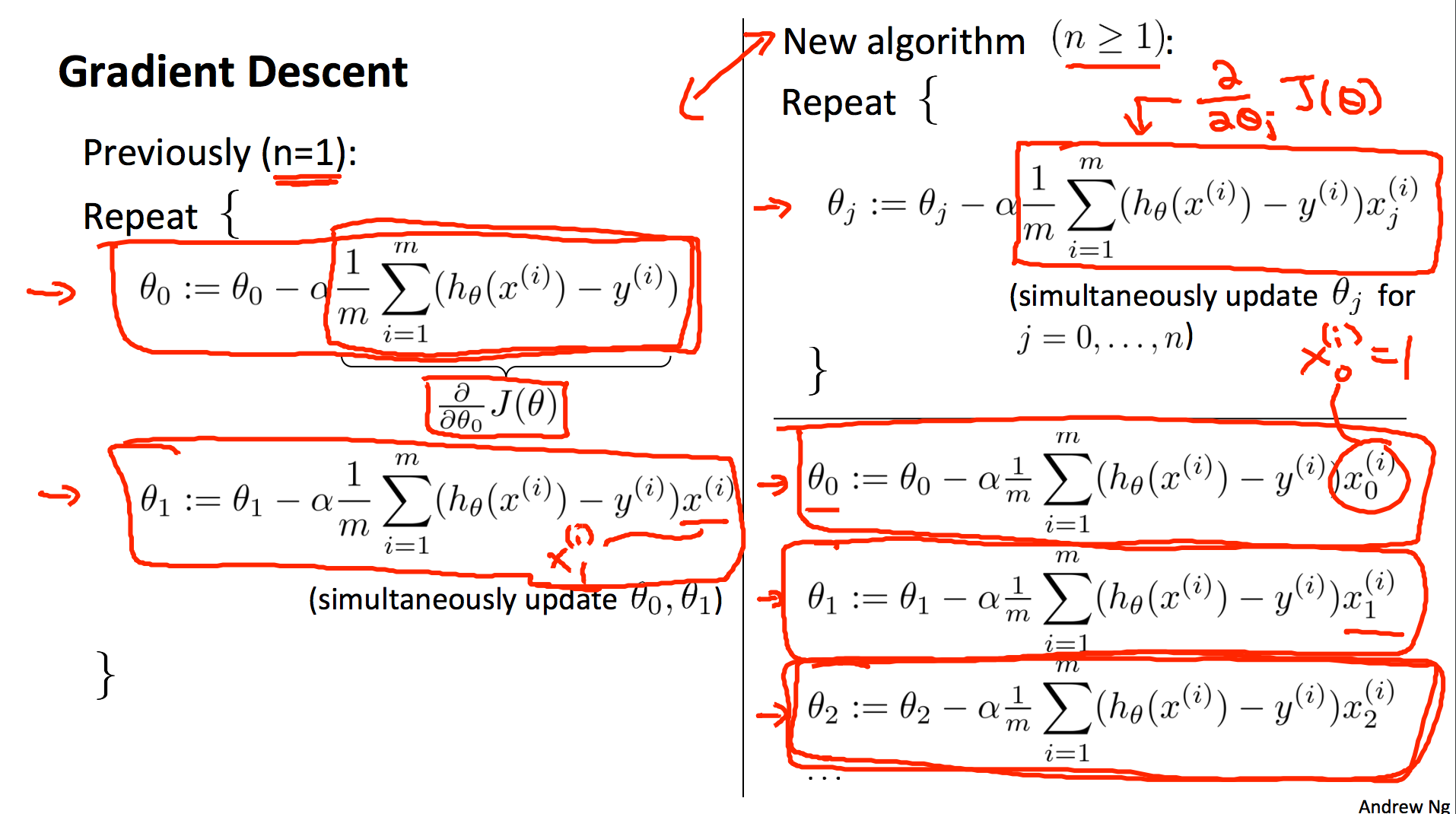
L2] Linear Regression (Multivariate). Cost Function. Hypothesis. Gradient
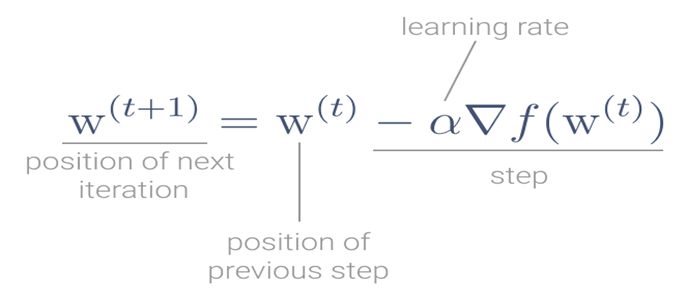
Optimization Techniques used in Classical Machine Learning ft: Gradient Descent, by Manoj Hegde

L2] Linear Regression (Multivariate). Cost Function. Hypothesis. Gradient
Solved] . 4. Gradient descent is a first—order iterative optimisation

nonlinear optimization - Do we need steepest descent methods, when minimizing quadratic functions? - Mathematics Stack Exchange

Gradient Descent algorithm. How to find the minimum of a function…, by Raghunath D

Solved 4. Gradient descent is a first-order iterative

Gradient Descent algorithm showing minimization of cost function

MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing

Task 1 Gradient descent algorithm: In this project

Non-Linear Programming: Gradient Descent and Newton's Method - 🚀
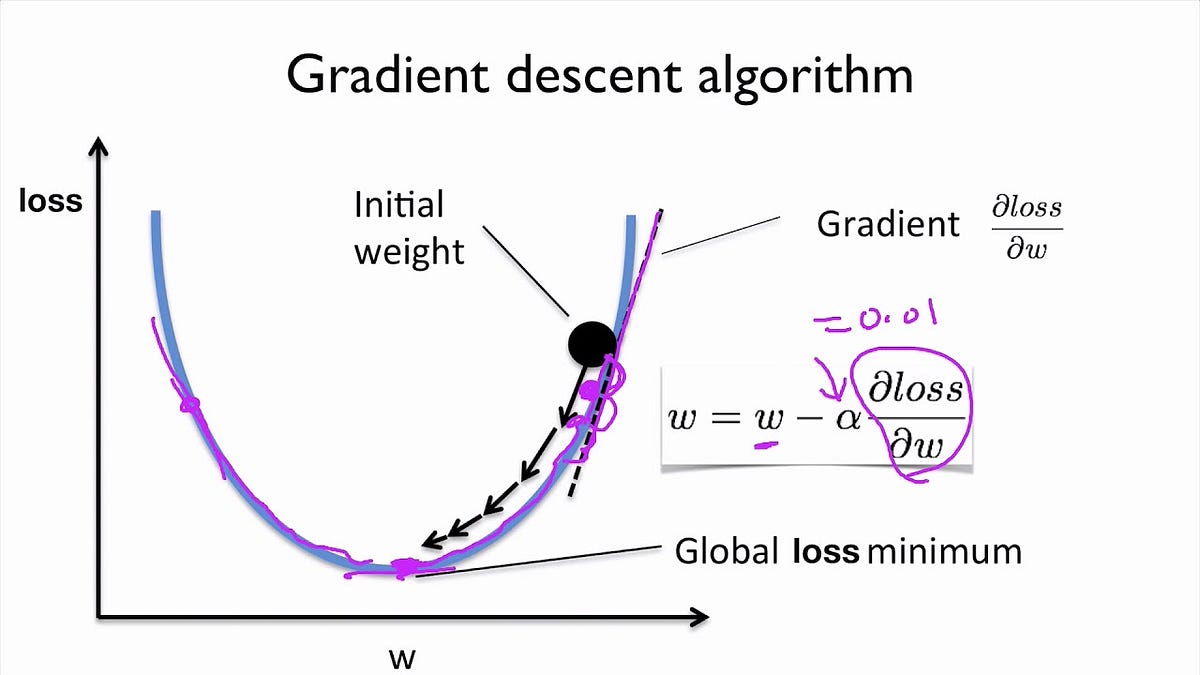
Linear Regression From Scratch PT2: The Gradient Descent Algorithm, by Aminah Mardiyyah Rufai, Nerd For Tech
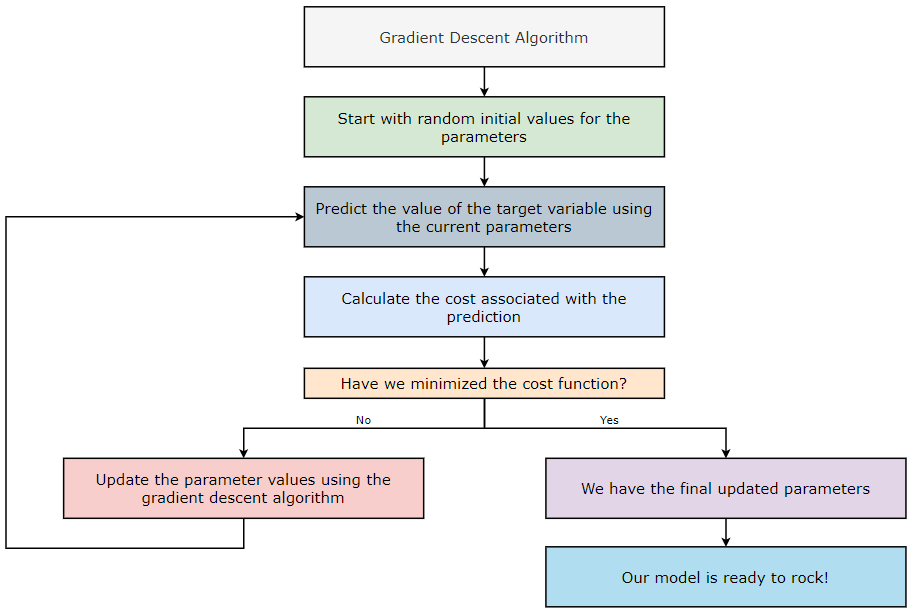
The Gradient Descent Algorithm – Towards AI
Recomendado para você
-
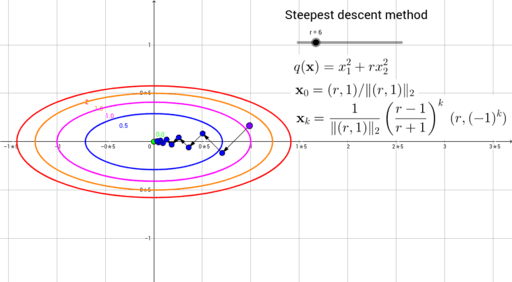 Steepest descent method for a quadratic function – GeoGebra13 abril 2025
Steepest descent method for a quadratic function – GeoGebra13 abril 2025 -
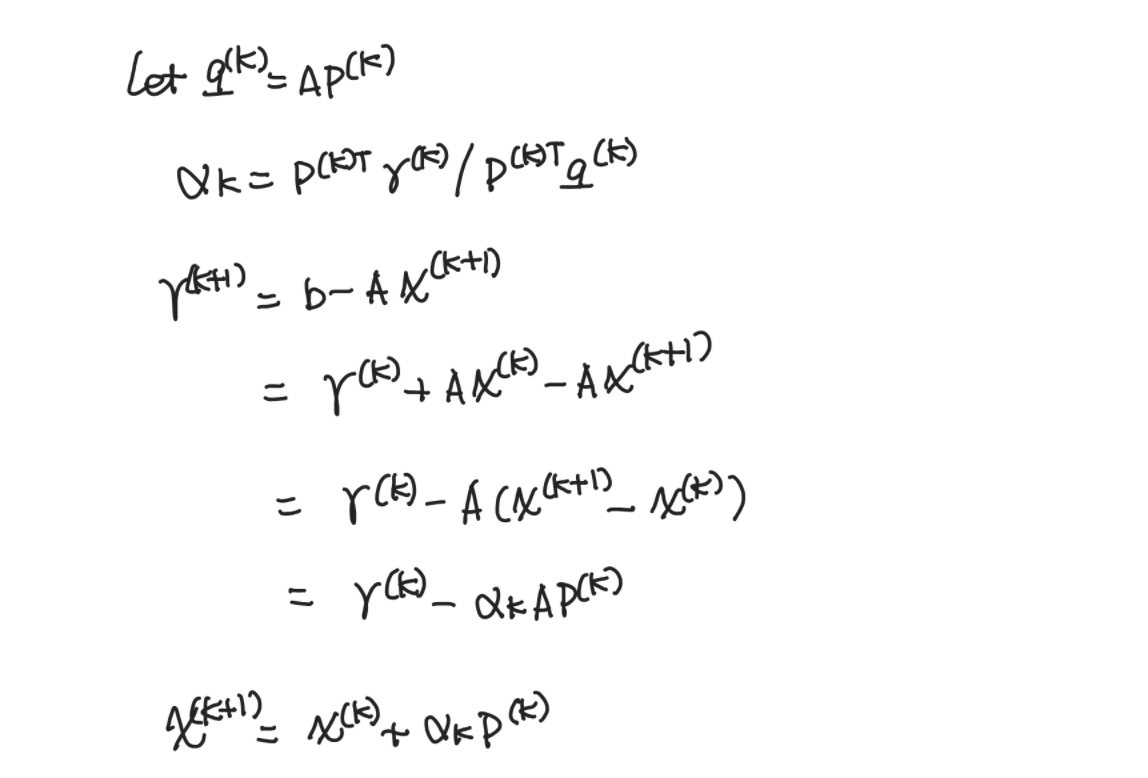 Descent method — Steepest descent and conjugate gradient, by Sophia Yang, Ph.D.13 abril 2025
Descent method — Steepest descent and conjugate gradient, by Sophia Yang, Ph.D.13 abril 2025 -
 Steepest Descent Method13 abril 2025
Steepest Descent Method13 abril 2025 -
 Solved (b) Consider the nonlinear system of equations z +13 abril 2025
Solved (b) Consider the nonlinear system of equations z +13 abril 2025 -
 Steepest descent method13 abril 2025
Steepest descent method13 abril 2025 -
 2 The steepest descent method: ) ( ) (k x and ) 2 ( ) ( ) ( k k k e x α13 abril 2025
2 The steepest descent method: ) ( ) (k x and ) 2 ( ) ( ) ( k k k e x α13 abril 2025 -
 The Steepest-Descent Method - ppt download13 abril 2025
The Steepest-Descent Method - ppt download13 abril 2025 -
 Using the Gradient Descent Algorithm in Machine Learning, by Manish Tongia13 abril 2025
Using the Gradient Descent Algorithm in Machine Learning, by Manish Tongia13 abril 2025 -
 Comparison descent directions for Conjugate Gradient Method13 abril 2025
Comparison descent directions for Conjugate Gradient Method13 abril 2025 -
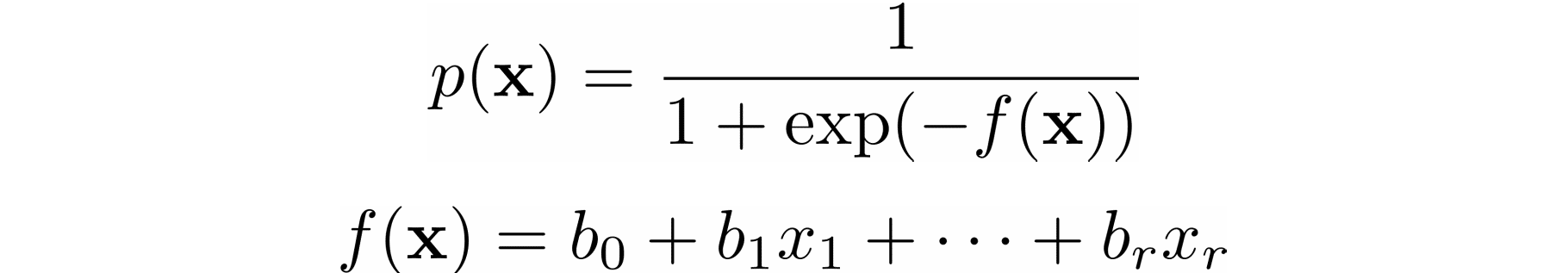 Stochastic Gradient Descent Algorithm With Python and NumPy – Real Python13 abril 2025
Stochastic Gradient Descent Algorithm With Python and NumPy – Real Python13 abril 2025
você pode gostar
-
 Ralph Love Ralph Lauren perfume - a fragrance for women 201613 abril 2025
Ralph Love Ralph Lauren perfume - a fragrance for women 201613 abril 2025 -
 Iori Yagami, KOF 2002 Fan remaster by theJUANLION on DeviantArt13 abril 2025
Iori Yagami, KOF 2002 Fan remaster by theJUANLION on DeviantArt13 abril 2025 -
 Miranda do Corvo: Apresentação do livro “Lendário – 100 Lendas da13 abril 2025
Miranda do Corvo: Apresentação do livro “Lendário – 100 Lendas da13 abril 2025 -
 The RZA Presents Afro Samurai Resurrection Vinyl Original Soundtrack13 abril 2025
The RZA Presents Afro Samurai Resurrection Vinyl Original Soundtrack13 abril 2025 -
 Gameteczone Usado Jogo Nintendo Switch Mario Tennis Aces - Nintendo Sã - Gameteczone a melhor loja de Games e Assistência Técnica do Brasil em SP13 abril 2025
Gameteczone Usado Jogo Nintendo Switch Mario Tennis Aces - Nintendo Sã - Gameteczone a melhor loja de Games e Assistência Técnica do Brasil em SP13 abril 2025 -
Combat Mode has Been Disabled, #fail #jumpscare #atomicheart #scp14713 abril 2025
-
 Call of Duty®: Mobile Tournament Mode – A Guide to a New13 abril 2025
Call of Duty®: Mobile Tournament Mode – A Guide to a New13 abril 2025 -
 Julianna Pena explains lack of trash talk on Season 30 of The Ultimate Fighter: I feel bad for the poor girl. You want me to continue to talk?13 abril 2025
Julianna Pena explains lack of trash talk on Season 30 of The Ultimate Fighter: I feel bad for the poor girl. You want me to continue to talk?13 abril 2025 -
 عالم ادوية يموت وينتقل لعالم اخر بقوة الحكام من اجل ان يساعد الناس13 abril 2025
عالم ادوية يموت وينتقل لعالم اخر بقوة الحكام من اجل ان يساعد الناس13 abril 2025 -
𝑳𝑨𝑺𝑻 𝑶𝑵𝑬! 🆚 Minnesota Invitational 🏟️ Jean K. Freeman Aquatic Center 📍Minneapolis, Minn. 🕗 8 a.m. PT: Swimming Prelims 🕚 11 a.m. PT:…13 abril 2025

